IL MOTO DEI SATELLITI

Newton partendo dalle leggi di Keplero riuscì a dedurre la legge di gravitazione universale e dimostro’ anche che , inversamente , dalla legge di gravitazione universale seguono le leggi di Keplero , a ulteriore conferma che il moto planetario è determinato dalla legge di gravitazione universale.

Alla luce della legge di gravitazione universale possiamo esaminare il moto di un corpo di massa m intorno ad un altro corpo di massa M molto più grande.

Orbite circolari

La velocità v del corpo di massa m sull’orbita di raggio r con centro in M per la seconda legge della dinamica dev’essere tale che la corrispondente accelerazione centripeta moltiplicata la massa m sia uguale alla forza di gravitazione alla distanza dal centro di M del punto in cui si trova m , cioè alla distanza r

Si ha perciò :

da cui risolvendo rispetto a v :

poiché la velocità può essere espressa dalla relazione

in cui T e il periodo di rivoluzione del pianeta o satellite considerato di massa m , l’equazione del moto può anche esprimersi nella forma :

Pertanto il rapporto tra il quadrato del periodo di rivoluzione e il cubo del raggio è una costante al variare di m per un fissato valore di M.

I satelliti terrestri e le velocità’ cosmiche

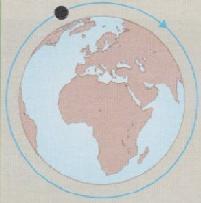
Newton dimostrò che qualsiasi grave , purché sia lanciato con velocità opportuna , diventa un satellite artificiale della Terra , per effetto della forza di gravità con cui viene attratto dalla Terra.

Finché la velocità di lancio è inferiore a una velocità critica , detta 1° velocità’ cosmica , la traiettoria del satellite è un’ellisse che interseca la superficie terrestre e della quale un fuoco coincide con il centro della Terra.

Se la velocità di lancio è uguale alla 1° velocità’ cosmica , pari a 7,9 km/s , il satellite si muoverà intorno alla Terra su un’orbita circolare con raggio uguale al raggio terrestre.

L’orbita circolare diventa ellittica con un fuoco nel centro della Terra se la velocità di lancio è compresa tra 7,9 km/s e 11,2 km/s , detta 2° velocità’cosmica o velocità di fuga.

Per un satellite che ruota intorno alla Terra valgono tutte le relazioni trovate per l'orbita circolare di una massa m nel campo gravitazionale generato dalla massa M in cui ora la massa M diventa la massa della Terra mentre m quella del satellite.
L'equazione diventa perciò':

Calcolo della prima velocità' cosmica

Per la seconda legge della dinamica si ha l'equazione

e risolvendo rispetto a v :

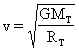
Sostituendo i valori numerici si ottiene:

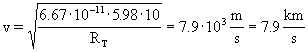
Calcolo della seconda velocità' cosmica

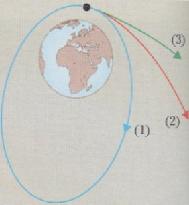
Per il calcolo della seconda velocità cosmica, osserviamo che l'energia totale all'infinito è nulla in quanto è zero non solo l'energia cinetica ( per definizione di velocità' di fuga ) ma anche l'energia potenziale. Ne segue che, per il principio di conservazione dell'energia l'energia totale è nulla anche sulla superficie terrestre, cioè alla distanza dal centro della Terra. Possiamo perciò scrivere:

da cui si ricava la velocità di fuga:

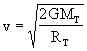
Eseguendo il calcolo numerico si ha:

Satelliti Geostazionari

Un notevole progresso scientifico si è avuto con la messa in orbita di satelliti geostazionari o sincroni che trovandosi rispetto alla Terra sempre nella stessa posizione, permettono di realizzare telecomunicazioni intercontinentali nei due sensi.
Se indichiamo con h la quota del satellite sincrono, per la seconda legge della dinamica si ha:

Da cui si ricava:

in cui il periodo T è pari a 1 giorno.
Sostituendo i valori numerici si ottiene:

Bibliografia

Physica 1 ( Antonio Caforio ; Aldo Ferilli- Le Monnier)

di Stefano Galimberti

<< indietro