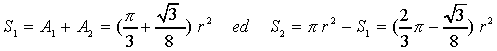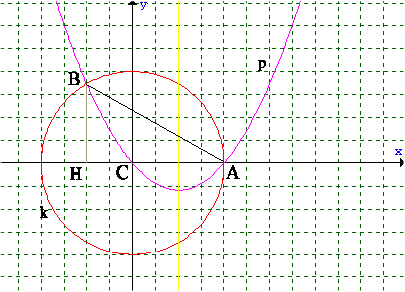
Nel sistema di riferimento indicato in figura l'equazione della circonferenza k risulta

Essendo AB il lato del triangolo equilatero inscritto in k, si avrà :

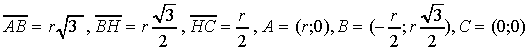
a) La parabola p, passando per l'origine C degli assi cartesiani e per A, ha equazione del tipo

Imponendo il passaggio per B si ottiene il valore di a e risulta:

________________________________________________________________

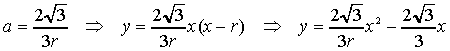
b)

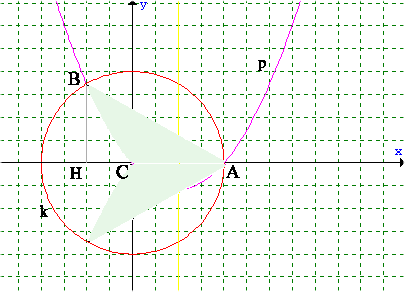
Il volume richiesto V si ottiene togliendo dal volume V₁ del cono avente per raggio di base BH e altezza AH il volume V₂ del solido generato dalla rotazione completa del triangolo mistilineo BHC intorno all'asse x. Si ha:

_________________________________________________________________________

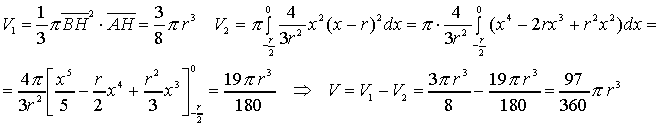
c)

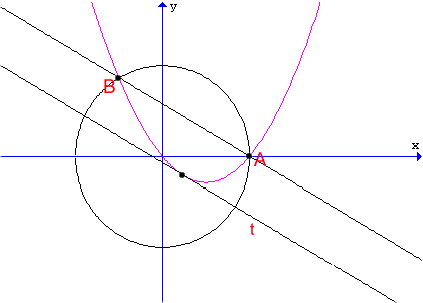
La retta AB ha coefficiente angolare

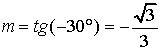
L'equazione della retta t, parallela ad AB, è quindi del tipo

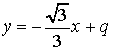
Mettendo a sistema questa equazione con quella della parabola e ponendo uguale a zero il discriminante dell'equazione di secondo grado risolvente, si ottiene

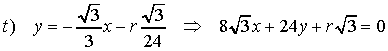
La distanza tra le due rette parallele AB e t si può ottenere calcolando la distanza del punto A=(r;0) dalla retta t ; si ottiene :

______________________________________________________________

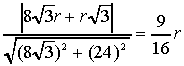
d) Ponendo a sistema l'equazione della parabola e quella della circonferenza, si perviene all'equazione risolvente:

che, in base ai dati di partenza, si abbassa di grado con x=r ed x=-r/2; applicando la regola di Ruffini si ottiene:

Poiché il discriminante dell'equazione 4x²-6rx+6r²=0 è negativo, si può concludere che la circonferenza e la parabola non hanno altre intersezioni oltre ad A e B.

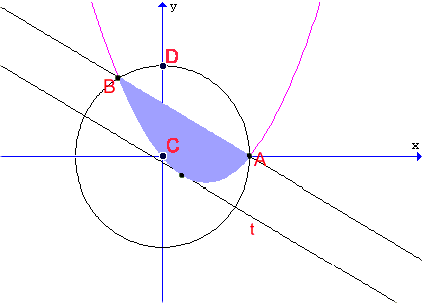
Poniamo

- A₁ = area segmento circolare ABD

- A₂ = area segmento parabolico ABC.

Risulta:

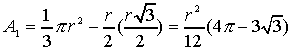
L'area del segmento parabolico si può calcolare mediante il teorema di Archimede; risulta:

Dette S₁ ed S₂ le due aree richieste, risulta: