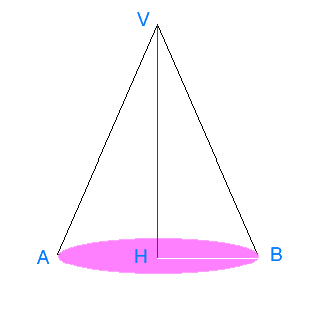
In base alle ipotesi risulta

2 h + 2 R = 2 L

avendo indicato con R il raggio di base e con 2L la lunghezza assegnata.

Il volume del cono è dato da

Essendo R + h = L = costante

il prodotto R²h è massimo quando :

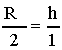
(Si ricorda la seguente proprietà: se la somma di due grandezze positive è costante il prodotto di due loro potenze è massimo quando le basi sono proporzionali agli esponenti).

Il volume in questione è quindi massimo quando

Allo stesso risultato si può pervenire utilizzando le derivate:

posto R=x otteniamo h=L-x e quindi il volume è dato da:

che è massimo quando lo è

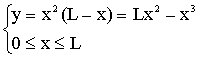
La funzione da ottimizzare è continua in un intervallo chiuso e limitato, quindi (per il teorema di Weierstrass) ammette massimo e minimo assoluti ed essi sono da ricercare agli estremi dell'intervallo o nei punti stazionari (punti a derivata nulla), non essendoci punti singolari (punti di non derivabilità). Risulta:

y' = 2 L x - 3 x² = 0 per x = 0 o per x = (2L)/3.

Calcoliamo il valore di y in quest'ultimo punto e agli estremi dell'intervallo:

y(2L/3) = (4/27) L³

y(0) = 0

y(L) = 0

e pertanto il massimo si ha quando x = R = (2 L ) / 3, come trovato per via sintetica.

Vediamo ora se il cono di volume massimo ha anche la massima area laterale.

Indicata con a l'apotema del cono, l'area S è data da:

che è massima quando lo è:

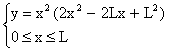
Calcoliamo la derivata prima:

y' = 8x³ - 6 L x² + 2 x L² = 2 x ( 4 x² - 3 L x + L² )

Il trinomio 4 x² - 3 L x + L² , avendo il discriminante negativo è sempre positivo, quindi la derivata si annulla solo, per x=0 ed è positiva altrove. Calcolando il valore di y per x=0 e per x=L si scopre che la funzione ammette il massimo assoluto in x=L , quando il cono degenera in un cerchio di raggio L.

Pertanto quando il volume del cono è massimo non si ha la massima area laterale.

Posto HK= x per trovare il raggio di base del cilindro consideriamo la similitudine fra i triangoli AVH ed EVK ; risulta:

Il volume del cilindro inscritto nel cono di volume massimo è quindi dato da

che è massimo quando lo è

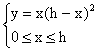
Risulta y'=3 x² - 4 h x + h²

che si annulla per x=h ed x=h/3. Il massimo richiesto si ha per x=h/3, ovvero quando l'altezza del cilindro è uguale a L/9.

Allo stesso risultato si può arrivare in modo sintetico:

essendo x ed h-x due quantità positive con somma costante, il prodotto x(h-x)² è massimo quando x=(h-x)/2, da cui x=h/3 come prima.

Il teorema di cui si chiede la dimostrazione è un noto corollario del teorema di Lagrange.

Applicando il teorema di Lagrange all'intervallo [x';x"] si ha:

dove c è un punto interno all'intervallo. Risultando

deve essere

come si voleva.

Che la condizione espressa dal teorema sia sufficiente ma non necessaria lo si può facilmente verificare analizzando, per esempio, la funzione di equazione

Tale funzione è chiaramente decrescente eppure la derivata non è sempre negativa, essendo nulla per x=0.