ESAME DI STATO DI LICEO
SCIENTIFICO
a.s. 2002/2003
CORSO SPERIMENTALE
SESSIONE SUPPLETIVA
Autonomi gruppo 1
Il candidato risolva uno dei
due problemi e 5 dei 10 quesiti in cui si articola il questionario.
PROBLEMA 1.
In un piano,
riferito ad un sistema di assi cartesiani ortogonali (Oxy), sono assegnate le parabole di
equazione:
y = (a –
1) x2 – 2 a x + a2 ,
dove a è un parametro reale
diverso da 1.
a)
Determinare quali tra esse hanno punti in comune con l’asse x e quali no.
b) Trovare le
due parabole che hanno il vertice in un punto di ascissa a.
c)
Stabilire se le due parabole trovate sono congruenti o no, fornendo un’esauriente
spiegazione della risposta.
d)
Scrivere l’equazione del luogo geometrico L dei vertici delle parabole assegnate e
disegnarne l’andamento dopo averne determinato in particolare asintoti, estremi e
flessi.
e)
Calcolare l’area della regione finita di piano delimitata dalla curva L e dalla retta
di equazione y=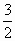 . .
|
PROBLEMA 2.
In un
trapezio rettangolo ABCD, circoscritto ad un cerchio, AB è la base maggiore, CD la minore
e BC il lato obliquo. Le misure, considerate rispetto alla stessa unità di misura, del
raggio del cerchio e del perimetro del trapezio sono nell’ordine 2 e 18.
a)
Calcolare le misure dei lati del trapezio.
b)
Riferito il piano della figura ad un conveniente sistema di assi cartesiani (Oxy),
scrivere le coordinate dei vertici del trapezio.
c)
Determinare l’equazione della circonferenza inscritta nel trapezio.
d)
Trovare le coordinate dei punti in cui questa circonferenza tocca i lati del trapezio.
e)
Calcolare le tangenti degli angoli interni del quadrilatero avente per vertici i suddetti
punti di contatto.
|
QUESTIONARIO.
1)
Nota la lunghezza di una corda di un cerchio di dato raggio, calcolare quella della corda
sottesa dall’angolo al centro uguale alla metà di quello che sottende la corda data.
[Nota –
La risoluzione del problema è stata usata da Tolomeo, II sec. d.C., per la costruzione di
una tavola trigonometrica in maniera equivalente alla nostra formula di bisezione del
seno.]
2)
Nello spazio ordinario sono dati due piani a , b ed una retta r. Si sa che r
è parallela ad a e perpendicolare a b . Cosa si può concludere circa la posizione
reciproca di a e b ? Fornire un’esauriente spiegazione della
risposta.
3)
Il dominio della funzione f(x) = è l’insieme degli x reali tali che: è l’insieme degli x reali tali che:
|
A) x£ 0 e/o x>2; B) x£ 0 e/o x³ 2; C) x=0 e/o x>2; D) x=0 e/o
x³ 2.
Una
sola risposta è corretta: individuarla e fornire un’esauriente spiegazione della
scelta operata.
4)
Si consideri un polinomio di grado n³ 2
nella variabile reale x con coefficienti reali. Dimostrare che condizione necessaria e
sufficiente affinché esso ammetta due zeri uguali al numero reale a è che il valore del polinomio e quello della sua
derivata prima si annullino per x=a .
5)
Stabilire se esistono i limiti della funzione f(x) = 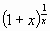 per: per:
|
a) x ® +¥
; b) x ® - ¥
; c) x ® 0 ,
e, in caso di risposta
affermativa, determinarli.
6)
Dimostrare che la derivata, rispetto ad x, della funzione:
|
f(x) = arcsen
x
è la
funzione:
f ’(x) =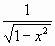 .
.
7)
Utilizzando il procedimento preferito, dimostrare la formula che fornisce l’area
della regione piana racchiusa da un’ellisse di semiassi noti.
Servendosi
della calcolatrice (o eventualmente di tavole logaritmiche) calcolare un valore
approssimato della soluzione della seguente equazione in x:
|
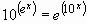 ,
,
dove e è la base dei
logaritmi naturali.
9)
La funzione reale di variabile reale f(x) è derivabile in ogni x per cui risulti -1£ x£
0; inoltre f(0)=0 e -1£ f ’(x)£ 0 in ogni x dell’intervallo –1<x<0.
Stabilire in modo esauriente se è vero o falso che risulta 0£ f(-1)£ 1.
10)
Considerata l’equazione in x:
a x2
+ b x + c = 0 ,
dove a, b, c
sono numeri reali qualsiasi, con a¹ 0,
scrivere un algoritmo che ne determini le soluzioni reali e le comunichi, esaminando tutti
i casi possibili.
|
___________________________
Durata massima della prova:
6 ore.
È consentito soltanto
l’uso di calcolatrici non programmabili.
Non è ammesso lasciare
l’aula degli esami prima che siano trascorse tre ore dalla dettatura del tema.
![]() .
.