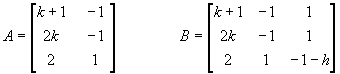
Maturità sperimentale 1998- Soluzione quesito 2
a)
Analizziamo la matrice A dei coefficienti e la matrice B completa:
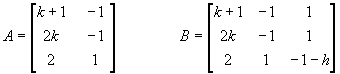
Affinchè il sistema ammetta soluzioni è NECESSARIO che sia det B = 0;
risultando det B = h(1-k) è NECESSARIO che sia h=0 vel k=1.
(N.B. Tali condizioni non sono sufficienti, perchè potrebbe essere rango(A)<rango(B), per esempio 1 e 2).
Analizziamo quindi i vari casi:
h=0
Si scopre che in tal caso il rango di A è 2 per ogni valore di k; quindi, essendo ovviamente il rango di B anch'esso 2, il sistema è compatibile e, per il teorema di Rouchè-Capelli, ammette 1 soluzione :|
(n: numero incognite, r: rango comune ad A e B)
che vuol dire infinite soluzioni dipendenti da zero parametri, ovvero una sola soluzione
k=1
Anche in tal caso il rango di A è 2 e pertanto si giunge alla stessa conclusione del caso precedente.
In conclusione:
il sistema ammette soluzioni (sempre 1) solo quando h=0 v k=1
b)
r) (k+1)x-y-1=0
s) 2kx-y-1=0
t) 2x+y+1+h=0
Notiamo che:
r ed s sono parallele se k+1=k, quindi k=1;
r e t sono parallele se k+1=-2, quindi k=-3;
s e t sono parallele se 2k=-2, quindi k=-1.
Inoltre:
Per k=1 r ed s coincidono, in tutti gli atri casi hanno in comune il punto A=(0;-1);
Quando il sistema ammette soluzioni (sempre 1) le tre rette, aventualmente in parte coincidenti, appartengono allo steso fascio proprio.
Si hanno le seguenti possibilità:
h=0 e k=1: r ed s coincidenti, t incidente;
h=0 e k=-1: s e t coincidenti r incidente;
h=0 e k=-3: r e t coincidenti. s incidente;
h=0 e k¹
1, -1, -1 : r, s e t distinte e passanti per A.
k=1: r ed s coincidenti, t incidente per ohno valore di h.
c)
Il sistema non ammette soluzioni per h¹ 0 e k¹ 1; le tre rette individuano un triangolo quando non ce ne sono mai due parallele, e ciò avviene se k¹ -1,-3.
d)
Sia h=1 ( e k¹ +1, -1, -3);
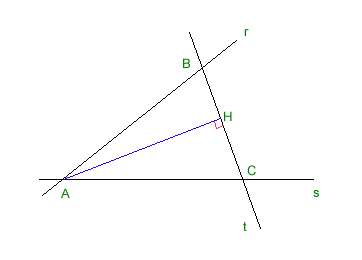
L'area richiesta è data da:
e risulta:
A=(0;-1); B=(-1/(k+3);(-4-2k)/(k+3)); C=(-1/(2k+2); (-2k-1)/(k+1));
Calcolando la distanza AH di A dalla retta t :
e la distanza tra B e C, si ottiene:
(con k¹ +1, -1, -3).
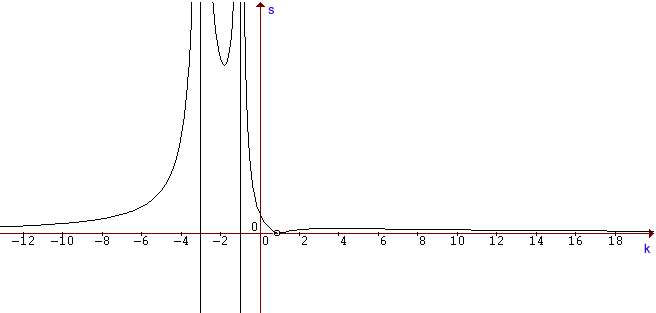
Per rappresentare s=s(k) è sufficiente studiare la funzione
la funzione richiesta si otterrà mediante l'operazione
che che si ottiene dal grafico di f(x) ribaltando rispetto all'asse delle x la parte negativa ed eseguendo una contrazione verticale di rapporto 1/4.
