
IL MODELLO DI FELIX KLEIN (1849-1925)

In tale modello si fissa una conica K irriducibile (per comodità un'ellisse o una circonferenza) e si danno le seguenti interpretazioni dei concetti primitivi:
Si costruisce un modello di geometria che soddisfa tutti gli assiomi della geometria euclidea (in una forma più moderna data da Hilbert) tranne il quinto e per la quale valgono le prime 28 proposizioni del I libro degli Elementi: il quinto postulato è quindi indimostrabile a partire dai primi quattro postulati e dalle prime 28 proposizioni, quindi è indipendente da essi; una geometria basata sui primi quattro postulati e sulle prime 28 proposizioni non presenta alcuna contraddizione logica.
Ma vediamo come si procede.
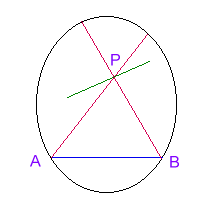
Le due rette PA e PB dividono le rette che intersecano la retta AB da quelle che non la intersecano; vi son perciò infinite rette passanti per P parallele ad AB; seguendo la dfinizione di Hilbert si chiamano però parallele le rette PA e PB, le "separatrici" delle rette parallele da quelle non parallele.
Pertanto:
"Per un punto esterno ad una retta passano due rette parallele alla retta data".
La geometria non euclidea in cui vale il precedente postulato al posto del quinto di Euclide è detta "geometria iperbolica".
N.B. Un altro modello di geometria iperbolica viene sviluppato da Poincarè: in tale modello si fissa una circonferenza K; si chiama punto un punto interno alla circonferenza; si chiama retta l'insieme dei punti di una circonferenza perpendicolare a K che sono interni a K.