IL LIBRO 1

Il LIBRO I degli Elementi è il più poderoso ed in esso si trova praticamente tutta la geometria piana che si studia a scuola. Contiene 23 termini (pseudo-definizioni), 5 postulati e 5 nozioni comuni.

Vediamo alcuni "termini":

1) Punto è ciò che non ha parte

2) Linea è una lunghezza senza larghezza

.............

23) Parallele sono le rette di un piano che, prolungate da tutte e due le parti, da nessuna di esse si incontrano.

Ai termini del primo libro seguono nel testo originale i 5 postulati:

1. "Si ammette di poter condurre da qualsiasi punto ad ogni altro punto una linea retta ;"
2. "e che ogni retta terminata si possa prolungare continuamente per dritto;"
3. "e che con ogni centro e con ogni distanza si possa descrivere un circolo;"
4. "e che tutti gli angoli retti siano uguali tra di loro;"
5. "e che se una retta, incontrandone altri due, forma angoli interni da una stessa parte minori di due angoli retti, le due rette prolungate continuamente si incontrano dalla parte in cui sono gli angoli minori di due retti".

Il postulato n. 5, noto come IL QUINTO POSTULATO DI EUCLIDE o POSTULATO DELLE PARALLELE è quello caratteristico della geometria euclidea e da esso segue la dimostrazione dell'esistenza di almeno una parallela per un punto ad una retta data; da questo postulato e dalla proposizione 29 del libro 1 segue poi l'unicità della suddetta parallela.

Vediamo qualche sempio di "nozione comune":

1) Cose uguali ad una stessa cosa sono uguali;

2) il tutto è maggiore della parte;

.........

La prima proposizione di Euclide in cui si introduce il concetto di rette parallele, senza ancora ricorrere al quinto postulato, è la n. 27.

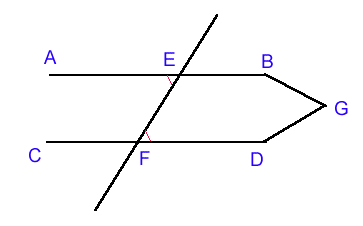
Proposizione 27

Se una retta, cadendo su due rette, fa gli angoli alterni interni uguali fra loro, le due rette saranno parallele fra loro.

Cadendo sulle due rette AB, CD, la retta EF formi gli angoli alterni AEF, EFD uguali fra loro. Dico che AB è parallela a CD.

Infatti se così non fosse, AB e CD prolungate (postulato 2) si incontrerebbero o dalla parte di B e D, o dalla parte di A e C.

Si prolunghino e si supponga che si incontrino nel punto G dalla parte di B e D. Allora, nel triangolo GEF, l'angolo esterno AEF risulterebbe uguale all'angolo interno ed opposto EFG, il che è impossibile (nella prop. 16 si dimostra il cosiddetto teorema dell'angolo esterno).

Dunque AB e CD, prolungate, non si incontrano dalla parte di B e D; analogamente si può dimostrare che esse non si incontrano neppure dalla parte di A e C. Ma allora, per il termine 23, le due rette sono parallele. Come dovevasi dimostrare.

Questo teorema rappresenta una vera vittoria sull'infinito, poichè il confronto di ciò che avviene al finito (l'uguaglianza tra due angoli) permette di dedurre una proprietà relativa ad un qualcosa che accade all'infinito.

Notiamo che le prime 27 proposizioni del primo libro degli Elementi non usano il suddetto Quinto postulato e pertanto sono vere anche nelle geometrie non euclidee. Ma il quinto postulato, lasciato accuratamente in disparte fino a questo momento, deve essere necessariamente utilizzato per invertire la prop. 27.