Bolyai e Lobacevskij

Il procedimento seguito dai due matematici (con molta approssimazione espositiva) è il seguente.

Dati una retta AB e un punto P complanare ed esterno ad essa, sia PO la perpendicolare alla retta passante per il punto P. Si consideri ora un punto D sulla retta AB; per esso passerà la retta PD secante la retta data. Si faccia muovere il punto D nel verso OB in corrispondenza di ogni posizione occupata da D sulla retta, si otterrà una secante PD alla retta assegnata. Si consideri ora la distanza OD tendente all'infinito; troveremo in corrispondenza una retta PL che non intersecherà la retta AB, e che quindi sarà parallela ad OB.

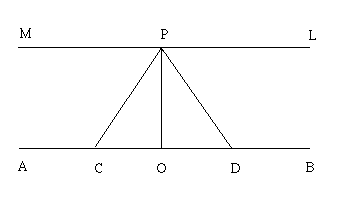
Si proceda in ugual modo dall'altra banda; anche in questo caso si troverà una retta PM non secante la retta data, e pertanto parallela ad OA.

Ora, secondo la geometria euclidea, PL e PM costituiscono un'unica retta parallela ad AB, e gli angoli OPL e OPM sono uguali e retti. Si assuma invece l'ipotesi dell'angolo acuto; allora PL e PM saranno due rette distinte, ed entrambe parallele ad AB pur senza essere equidistanti in ogni punto rispetto alla retta data! Quali sono le condizioni del loro parallelismo? Anzitutto bisognerà distinguere per ognuna delle due rette un proprio verso di parallelismo: e si dirà che PL è parallela ad OB e PM è parallela ad OA; inoltre ognuna di esse, pur prolungata all'infinito nel verso del parallelismo, non incontrerà mai la retta data, e la distanza da questa diminuirà infinitamente.

Da questa nozione di parallelismo discendono poi una serie di proprietà matematicamente dimostrabili. Ad esempio che l'angolo di parallelismo pigreco (OPL + OPM) è variabile in dipendenza dalla grandezza della perpendicolare PO; cioè diminuisce con l'aumentare della perpendicolare, e aumenta col diminuire della perpendicolare; perciò esso tende a zero quando la perpendicolare tende all'infinito; e tende a pigreco quando la perpendicolare tende a zero.

Inoltre, la distanza tra due rette parallele, ad esempio PL e OB, tende a zero nel verso del parallelismo, e invece tende all'infinito nel verso opposto.

Infine due rette parallele tra loro non avranno alcuna perpendicolare in comune; o meglio la avranno all'infinito, cioè là dove esse formano un angolo nullo.

Con ciò fu dimostrato che è possibile costruire un sistema geometrico logicamente coerente e rigoroso, a partire da una ipotesi prescelta, e che non solo non si dava un'unica geometria vera, quella euclidea, ma questa era anch'essa una costruzione basata su un'ipotesi preliminarmente scelta.